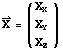 ,
,
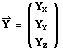 and
and
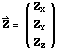
If the axes of the spacecraft reference frame with respect to a reference frame B are given by
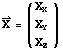 ,
,
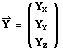 and
and
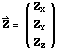
then the spacecraft attitude matrix with respect to reference frame B is defined by (see Wertz 1978 )
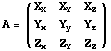 .
.
All supported reference frames are right handed and orthonormal i.e.
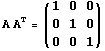 and
and  .
.
If 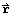 corresponds to a vector relative to reference frame B and
corresponds to a vector relative to reference frame B and
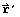 corresponds to the same vector in spacecraft frame then
the following equations hold:
corresponds to the same vector in spacecraft frame then
the following equations hold:
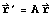 and
and  .
.
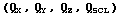 .
The attitude matrix that corresponds to a quaternion can be calculated by
.
The attitude matrix that corresponds to a quaternion can be calculated by
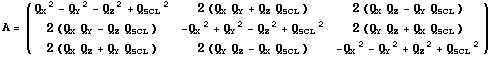
Note that the sign of the quaternion is ambiguous i.e.
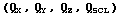 and
and 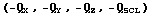 correspond to the same attitude matrix.
correspond to the same attitude matrix.
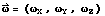 relative to inertial space.
The attitude rates are always expressed in spacecraft frame and are related to the attitude matrix by:
relative to inertial space.
The attitude rates are always expressed in spacecraft frame and are related to the attitude matrix by:
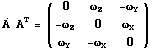
If a vector 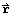 and the time derivative of the vector
and the time derivative of the vector
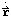 are given relative
to inertial space then the corresponding vectors in spacecraft frame
are given relative
to inertial space then the corresponding vectors in spacecraft frame
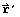 and
and 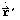 can be calculated by
can be calculated by
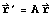 and
and 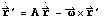 .
.
The calculation of all state vectors is based on the inertial position and velocity of
the objects relative to the solar system barycentre relative to EME2000.
If 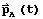 and
and 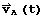 are the position and velocity of an object A and
are the position and velocity of an object A and
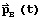 and
and 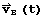 are the position and velocity vectors of an object B at
barycentric dynamical time (TDB)
are the position and velocity vectors of an object B at
barycentric dynamical time (TDB) 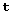 , then
the inertial state in equatorial frame of object A relative to object B is
calculated by
, then
the inertial state in equatorial frame of object A relative to object B is
calculated by
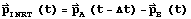 and
and 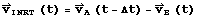 .
.
In case no light time correction is applied 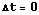 .
In case the light time correction
is applied
.
In case the light time correction
is applied 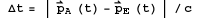 , where
, where 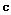 denotes the velocity of light.
denotes the velocity of light.
Transformation of the state vector in a reference frame with attitude matrix
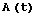 is performed by
is performed by
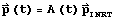 and
and 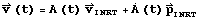 .
.
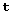 , is calculated as the angle between the vectors
, is calculated as the angle between the vectors
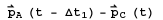 and
and 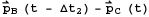 .
Light time correction for the calculation of an angle is supported.
.
Light time correction for the calculation of an angle is supported.
In case no light time correction
is applied 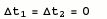 .In case the light time correction
is applied
.In case the light time correction
is applied 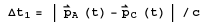 and
and 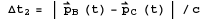 , where
, where 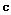 denotes the velocity of light.
denotes the velocity of light.
The allowed time range depends on the quantities that are to be retrieved. While planetary ephemerides are available for a long time span in the past and the future, spacecraft orbit and attitude files only cover a relative small time interval. If the requested time interval is out of range, a form is returned containing corrected start and end times.
Note that the number of rows in the table is limited. If a request results in a table that exceeds the maximum number of rows, a form is returned in which the end time is replaced by the latest end time that can be reached with the selected time step. In this case the user has to issue several requests in order to retrieve all required data.
| Mission | Ephemeris |
|---|---|
| Mars Express | DE405 planet ephemerides |
| Smart-1 | |
| Rosetta | |
| Venus Express | |
| Herschel | |
| Planck | |
| Gaia | INPOP10e planet ephemerides |
| Exomars | DE432 planet ephemerides |
| Bepi Colombo | not defined yet |
| Solo | not defined yet |
| Euclid | not defined yet |
The orbits of comet Churyumov-Gerasimenko and the fly-by asteroids were determined using Earth-based optical measurements on right ascension and declination and optical navigation data. The operational orbit of Deimos satellite is calculated using an analytical model (see Morley 1990). The Phobos ephemeris are taken from the JPL Horizons System.
The determination of spacecraft orbit is essentially based on a batch least square procedure taking into account radiometric tracking data provided by tracking stations on Earth (see DDID, Appendix H) and for Rosetta also optical navigation data are used. Note that due to this process the recent past is subject to small updates.
The spacecraft attitude is not reconstructed from telemetry, but is based on the attitude commanded to the spacecraft. In cases where the spacecraft body does not exactly follow the commanded attitude an offset is applied to the commanded attitude to compensate for the expected offset. Note that due to autonomeous spacecraft behaviour during certain modes (e.g. safe-modes) it is possible that the spacecraft attitude is unknown and therefore not available during these time intervals.
The spacecraft orbit and attitude data can also be accessed using the on-line forms. For the operational data set, the on-line form offers to retrieve data based on the spacecraft attitude i.e. attitude matrix, quaternion and rate. Additionally, it is also possible to retrieve state vectors relative to the spacecraft frame by selecting the option "spacecraft" in the corresponding dropdown-list. Note that for times during which the spacecraft attitude is unknown the returned table does not contain numeric data but the statement: "THE QUANTITY IS NOT AVAILABLE AT THIS TIME".
DDID, Appendix H: 2005, "Rosetta, Mars Express, Venus Express Mission Control System (MCS) Data Delivery Interface Document, Appendix H", RO/MEX/VEX-ESC-IF-5003, Issue 3.1. (This document is available for download )
HPOEID 2009 "Herschel/Planck Orbit Events File ICD", PT-CMOC-FD-ICD-2103, Issue 1.4. (This document is available for download )